The Buffon Problem
30 Jul 2022“Ethical Maths”, Buffon 1777
“Essai d’arithmétique morale” published in 177 by Georges-Louis Leclerc de Buffon, describes (and solves) an interesting problem 1. The problem is quite simple: drop a needle (or match, or small branch) onto a wooden floor (or other floor with parallel lines). What is the chance that the dropped item will cross a line on the floor?
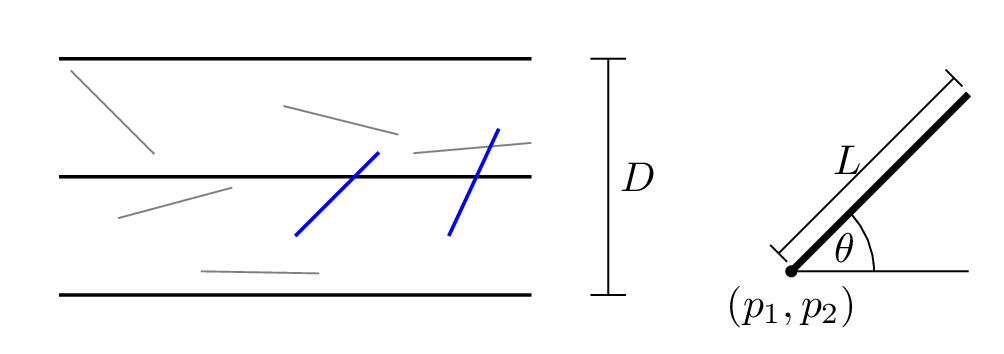
Fig. 1. Diagram describing the Buffon problem.
Fig. 1. above describes the problem. Grey lines are needles dropped but don’t cross a boundary, and blue lines cross boundaries. The needles are all of length $L$, gaps between boards of size $D$. A dropped needle has uniform angle orientation $\theta$ and uniform random position $(p_1, p_2)$.
How do we calculate the probability of crossing?
From statistical mechanics, we know to estimate probability by counting micro- and macro-states. In this context, a micro state is a combination of angle, and position (only y position though! x-position doesn’t matter), while macro-states are the total area of the “phase-space” - full swing of angles multiplied by the full gamut of positions. I’ve said area, but that’s not really right - we’re not measuring a $\rm length^2$ here, but it is a 2 dimensional measure of this space. I think the proper term would be a Lebesque measure.
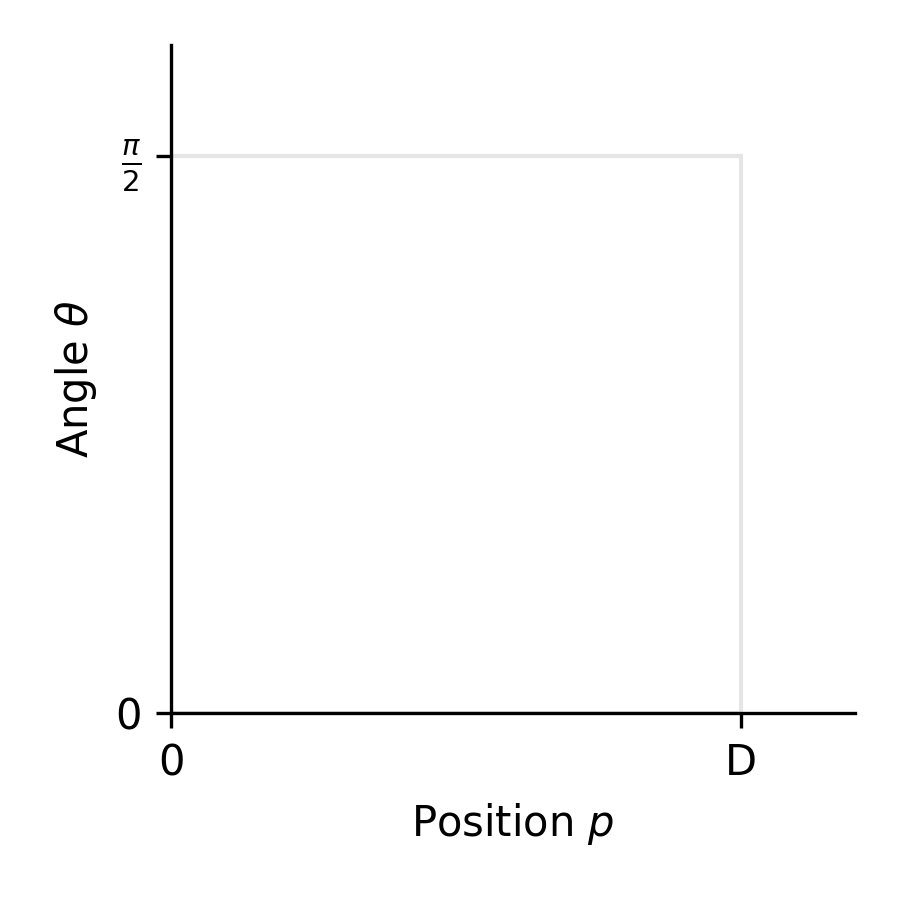
Fig. 2. Plot visualising the phase-space of concern.
Fig. 2. above shows the space we’re working with. Positions of a needle are along the x-axis, and the angle of the needle along the y-axis. We need to find the positions on this plot (combinations of position and angle) which result in a cross, and ones which result in a needle not crossing a border.
Let’s start thinking about this. If the angle is $0$ rad (the needle parallel to the borders), when will the needle cross a border? Well, assuming the needle has negligible width, it won’t. Therefore the maximum position a needle can have with an angle $0$ rad is $D$.
What if the angle is $\frac{\pi}{2}$ rad? Then the needle is perpendicular to the border. The needle will cross the border at a position $L$ from the border (position $D-L$ on Fig. 1), only if the distance between borders $D$ is greater than $L$ (or $L \leq D$). If this is not the case then the needle will always cross the border if perpendicular. So we diverge into two cases…
Case where $L \leq D$
What if the needle is between $\frac{\pi}{2}$ rad and $0$ rad? Now it will cross the border if needle is position a distance from the border equal to the the y-extent of the needle. To calculate the y-extent, let’s look back at Fig. 1. We just need to use trigonometry to calculate the height of the right-angled triangle made with the needle and the x-axis:
\begin{equation} \label{eqn:y} y = L\sin{\theta} \end{equation}
This function gives us the minimum distance from a border a needle must be placed in order to not cross it. (Or, the maximum distance from a border a needle can go in order to still cross it.)
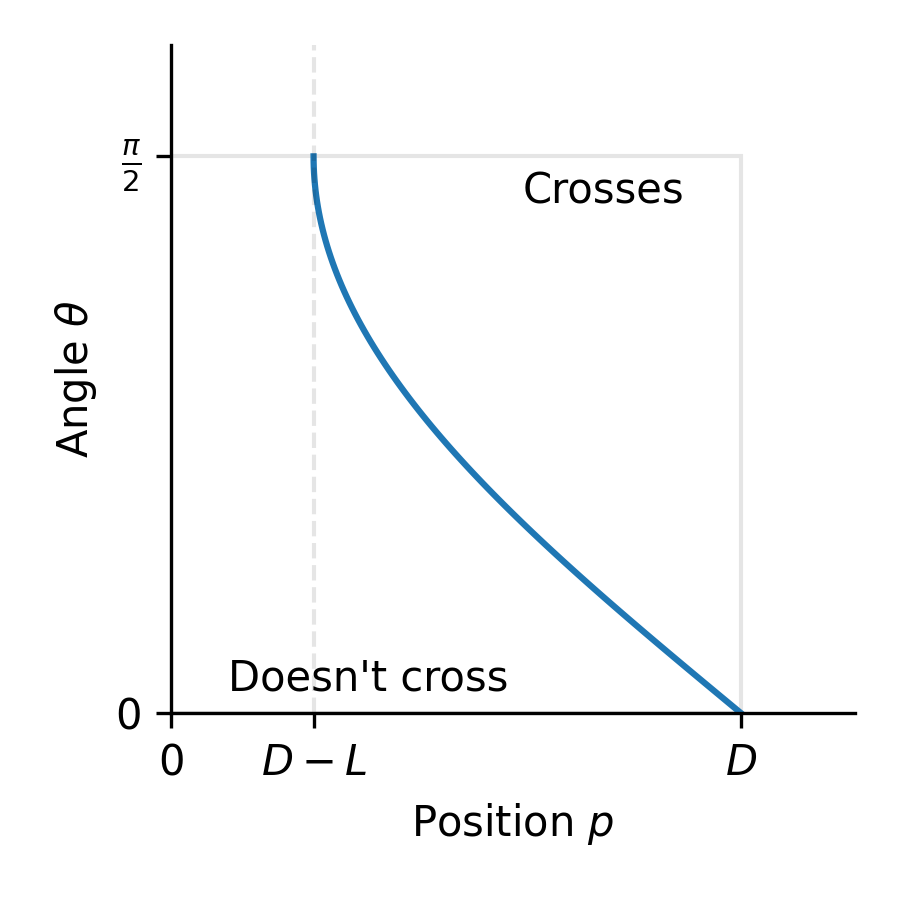
Fig. 3. Plot visualising the border between states where a needle crosses a border (right) or where the needle won't (left).
How to we get probability from this? Well, as I mentioned earlier, we need to count our states: we need to measure the area on Fig. 3. where a needle will cross a wall. This is simply given by the integral of Equation \eqref{eqn:y} above:
\begin{equation} \label{eqn:area-of-cross} A_{cross} = \int_0^{\pi/2}L\sin{(\theta)}d\theta = L \end{equation}
The total area is just the area of our rectangular phase space: \begin{equation} \label{eqn:total-area} A_{total} = \frac{\pi}{2}D \end{equation}
The probability of the dropped needle crossing a border is just the ratio of these areas: \begin{equation} \label{eqn:p} P_{cross} = \frac{A_{cross}}{A_{total}} = \frac{2L}{\pi D} \end{equation}
And that’s our solution for the case where border separation is greater than the needle length.
Case where $L > D$
Let’s think about this perpendicularly…
If we’re at a position $0$ from the border (i.e. position $D$ on Fig. 1), what is our minimum angle $\theta$ we can go without crossing the border? The needle could only be parallel to the border in this instance, $\theta=0$ radians.
Then, to the other extreme: If we’re $D$ units away from the border (i.e. position $0$ on Fig. 1), what angle can we make without crossing? We’re again limited by the y-extent given by Equation \eqref{eqn:y}, except we know that it crosses the y-axis as $L > D$: there must be some angle above which the needle always crosses the border. This is drawn out on Fig. 4 below:
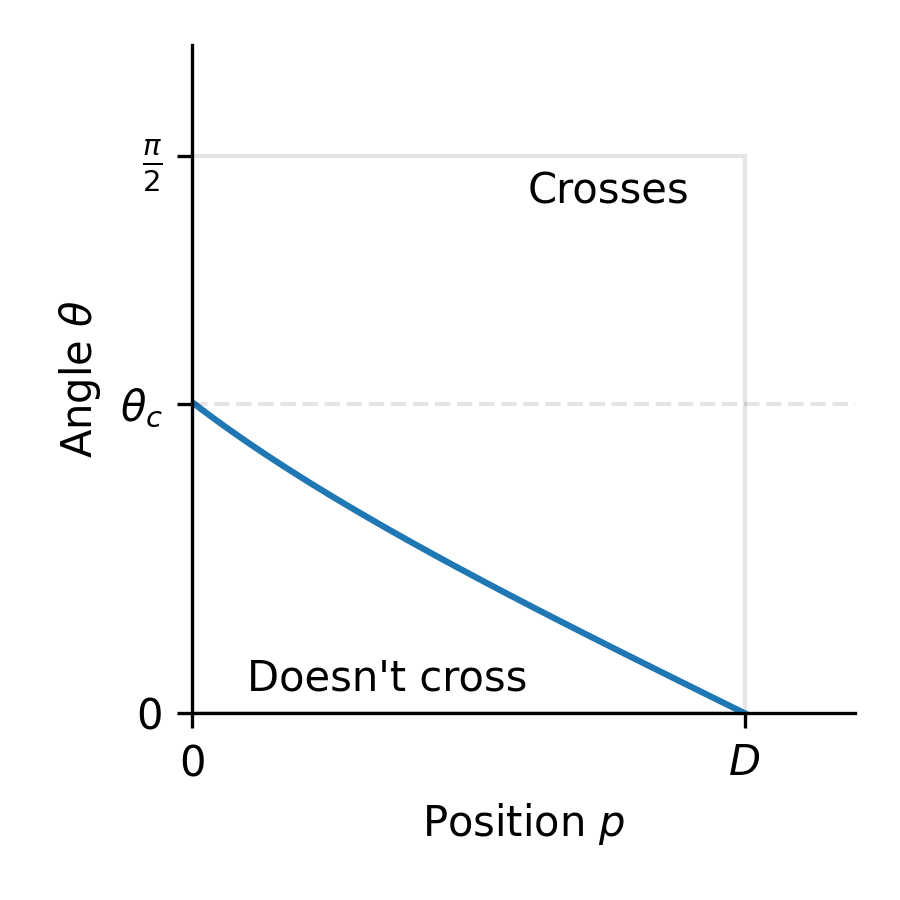
Fig. 4. Plot visualising the border between states where a needle crosses a border (above) or where the needle won't (below).
How do we get the area now? We have two options. We could integrate the same equation as before, but with different limits for $\theta$ of $0$ and $\theta_c$, and then adding on the area $D\left(\frac{\pi}{2} - \theta_c\right)$ (piecewise integral under the curve). Or, we could integrate with respect to position $y$ instead. We’d need to invert Equation \eqref{eqn:y} first:
\begin{equation} \label{eqn:yinv} \theta = \sin^{-1}{\left(\frac{y}{L}\right)} \end{equation}
And then integrate between $0$ and $D$ for the area where the needle doesn’t cross:
\begin{align}
\label{eqn:case-b-area-no-cross}
A_{no\ cross} &= \int_0^D\sin^{-1}{\left(\frac{y}{L}\right)}dy\nonumber \\
&= \left[\frac{y}{L}\sin^{-1}\frac{y}{L} + \sqrt{1 - {\left(\frac{y}{L}\right)}^2}\right]_0^D\nonumber\\
&= \frac{D}{L}\sin^{-1}\frac{D}{L} + \sqrt{1 - {\left(\frac{D}{L}\right)}^2} - 1
\end{align}
Hmm, not quite as elegant as the solution for the previous case.
