A Neural Network so simple its SINNfull
22 Feb 2020Motivation
A little while ago a friend of mine showed me his stock trading bot. The bot was given a bit of cash, a trading platform API key, and some simple rules to follow. If a stock was rising, buy. If it started to fall, sell. There were some buffer regions too, but that’s the gist. I asked him if he’d thought about incorporating some simple machine learning into the project, he seemed unsure, he liked the simplicity of his solution I think. I started thinking about doing this myself, it sounded like a fairly simple idea. And with high level tools like Tensorflow available, it should be fairly easy to implement.
However, I am quite interested in the nuts and bolts of machine learning, so I’m not going to use a high level package. I’m going to write my own neural network, hopefully learning a lot along the way.
I’ll start by looking at the basics and some of the history of machine learning and neural networks, then I’ll start going into the implementation details.
The result is on my github here.
Machine Learning
Machine Learning (ML) started life in the 1950s as Artificial Intelligence (AI). Programs were built to “reason” solutions to problems and identify patterns. Neural Networks are one of the first forms of practical artificial intelligence. They are modelled after the human brain: a series of neurons which are either “firing” or “quiet” depending on the value of other neurons or inputs. The first Neural Network machine was the SNARC built in 1951 and designed by influential computer scientist Marvin Minsky (unfortunately someone who was involved with that Epstein bloke).
 from: The Scientist article "Machine, Learning, 1951"
from: The Scientist article "Machine, Learning, 1951"
I have been trying to find a diagram of the SNARC, but no luck. It is probably in Minsky's PhD thesis (University of Princeton, 1954), but I cannot access a full version of the thesis. I have found a preview version, which only covers the first 24 pages.
Unfortunately, his thesis is proving really tough to track down. I can find no electronic copy anywhere, and no physical copies held by libraries willing to lend. Sigh. I hope to someday see the designs for the electro-mechanical learning machine!
Update March 2021: I have found a copy of the thesis! I'll need to devote a wee bit of time to pouring through it to find any interesting notes.
A Neural Network is a common machine learning method, but there are others: decision tree, hierarchical clustering, random forest, and even linear regression. (I found this article which has a lot more examples and some information on each.) I was surprised to see that linear regression made the list of “machine learning” algorithms. I guess I fell into the trap of AI: if I understand it then it can’t possible be real machine learning. (I definitely read about that somewhere but I can’t remember where.)
I’ll concentrate on the Neural Network, since it was one of the first, and is still a top contender today (through its new form: deep neural networks).
Neural Networks
A neural network is a network of neurons, of on-or-off binary signals, connected by “dendrites”. Neurons fire depending on the value of other neurons. This is modelled by weighting the value of the all the dendrites, edges, feeding into the neuron and summing. If the value passes a threshold, it is “firing”. Otherwise, it is “quiet”.
For a neuron \(j\), its value \(z_{j}\) is the sum of the values of the neurons input to it, weighted each by a factor \(w\) plus a bias:
\[z_{j} = \sum_{i=0}^{N }v_{i}w_{i} + bias\]The neuron value is then passed to an activation function which decides if the neuron fires or stays quiet. This stage is very important and affects the speed at which the network is trained and the effectiveness of the resulting network. Essentially the function determines how the neuron responds to input: how quickly a change in input changes the output, what thresholds there might be and so on. The training methods (briefly described later on) rely on gradients, as in the derivative of the output with respect to the input. The derivative of the activation function therefore plays an important role in training and must be chosen appropriately.
The “learning” aspect enters in by the evolution of the weights. Weights are chosen so that a set of sample inputs gives an expected sample output. These sample sets of inputs and outputs make up the training dataset. The process of changing the weights is called training, and this is the key part of the algorithm which teaches the net how to perform the desired task.
How are the weights found? The training set and expected output are key here: the output from the network compared with the expected output gives us an error. We can find the ideal weights by a few different methods, mediated by the error. Gradient descent is a common method. Imagine the weights of a network of two neurons. Plot the values of the error for each value of the two weights giving us a surface plot. We want to minimise the error, so we want to find the lowest amplitude location in our phase space (the landscape formed by our weights and error plot). Gradient descent describes the path of walking down this landscape to the minimum error by looking at the gradient of error with respect to the weights.
There are other methods of finding this minimum point, and we have reduced the complex task we want the network to do, to a minimisation problem! The task of recognising the genus of a lilly plant based on the shape of its leaves is just minimisation! Prediction of stock market prices is minimisation! Classification of animals into bird, cat, or other is minimisation!
Neural networks make it (relatively) easy to answer complex questions about data, however it doesn’t unveil much about the neural network’s “thinking” process. This is therefore a “black box” method, where the result is obtain by an unknown method and therefore must come with a pinch of salt. This pinch of salt is normally given as a confidence or certainty probability quoted alongside the answer.
 from Big Cat Rescue: Pharaoh the white serval
from Big Cat Rescue: Pharaoh the white serval
Even this has some caveats. The simple classification problem decribed above of splitting all animals into cat or bird or other becomes quite tough when we consider that many animals share aspects of cats. Is a serval a cat? What about a puma? Or a whippet? Are lions? What about seals? Many of these animals, purely via image analysis, could easily be confused for a cat via similar body shapes, or straight up close genetic make-up. The neural network used to answer the question needs to have complexity enough to fully encompass the solution. It needs to pick up on subtle differences between the serval and the cat, or it will mis-classify.
In the wall of text I have spouted here we can identify the two components of a successful neural network: sufficient complexity (i.e. enough neurons) to describe the solution fully, and good quality training data to create the pattern in the network.
Layers
I’ve talked about a Neuron, the nodes in our graph network, but how are the neurons connected?
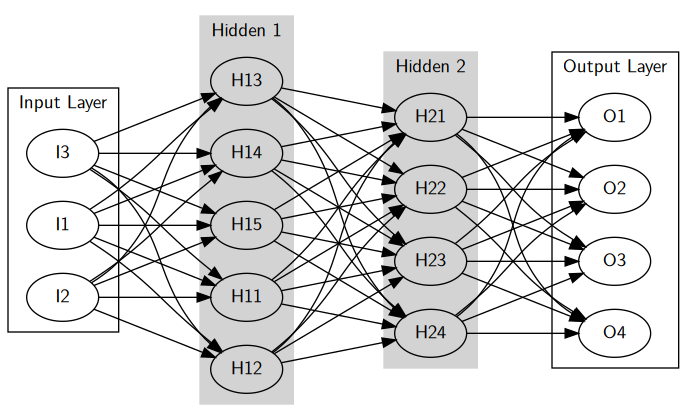 Neural network structure, input and output layers in white, hidden layers in gray. All connections are shown.
Neural network structure, input and output layers in white, hidden layers in gray. All connections are shown.
Neurons are grouped together in “layers”. Layers could be thought of as performing a specific action: taking input, performing an elaboration, or giving output. Each layer’s neurons are each connected to every neuron in the previous and subsequent layer.
We have an input layer, which takes information from somewhere and its neurons fire or are quiet depending on the values input.
There may or may not be layers in the middle called “hidden layers”. Neural networks can operate without a hidden layer, but many may perform better with one. I reason them as being used to filter out the inputs to give the important ones, or to convert the inputs into another form, internally.
Then there’s the output layer; this takes a pattern of neuron fires/quiets and produces a final value.
Deciding upon the number of neurons in a layer is an important design question that must be answered. There are, thankfully, some very smart people on the web with answers to these questions. This post on StackExchange has some handy information (although a little bit dated - question was posted 2011) about how to design a neural net layer.
Input layers should have enough neurons to capture the complexity of what is being analysed. If the input is an image, the input layer should be able to read the value of the pixels in the image. If the input is a number of features (“has ears”, “has wings”, “lays eggs”, etc), then there needs to be a neuron for each feature.
Output layers need neurons sufficient to convey the result. If output is a label, then a neuron per possible label is required. (This type of output is termed a “classifier”.) If output is a continuous number (e.g. a price, a size, a liklihood…) then a single output node is required. (Or, a node per desired value).
Hidden layers are the hard part. They’re difficult to reason: should the intermediary layers be intermediary in size? Or perhaps larger to emaphsise subtlety in the input? In fact, how many hidden layers should there be? None? Just the one? More?
The StackExchange post cites a book (“Introduction to Neural Networks for Java” by Jeff Heaton, 2008) which gives a little insight into the effect of hidden layers:
| Number of hidden layers | Effect |
|---|---|
| 0 | Only capable of representing linear separable functions or decisions. |
| 1 | Can approximate any function that contains a continuous mapping from one finite space to another. |
| 2 | Can represent an arbitrary decision boundary to arbitrary accuracy with rational activation functions and can approximate any smooth mapping to any accuracy. |
So more hidden layers, means more complexity that can be captured, and gives more confidence in fine-grain output. The first layer sees patterns in the input, subsequent layers see patterns in the patterns.
The wikipedia article on deep learning is quite good and has a lot of information. It include a fantastic image which gives an intuition for the hidden layers:
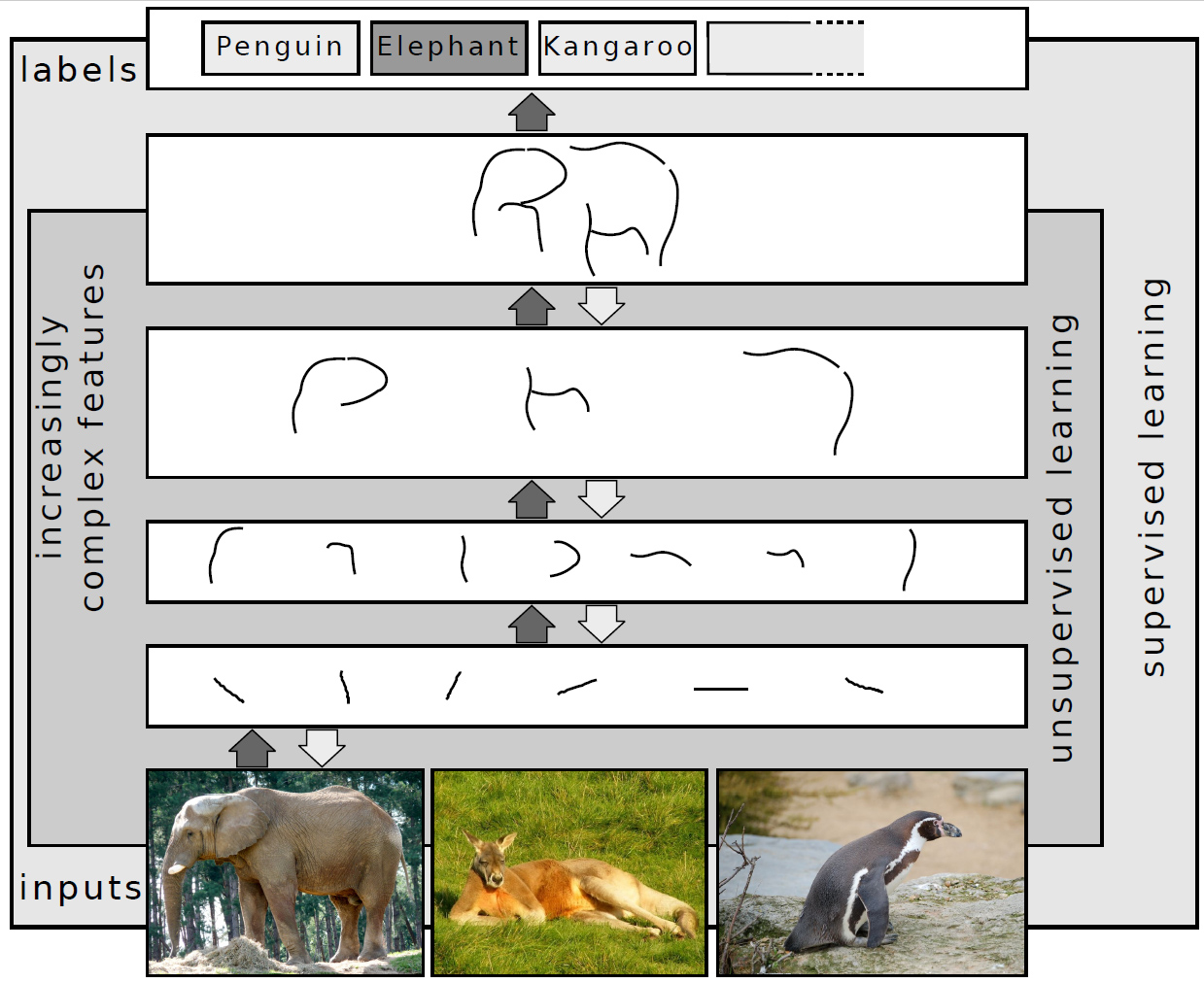 from Wikimedia Commons: Deep Learning.jpg by Sven Behnke CC-BY-SA 4.0
from Wikimedia Commons: Deep Learning.jpg by Sven Behnke CC-BY-SA 4.0
The first layer sees basic patterns: edges in the image. The second layer is taught to recognise shapes, third then recognises an ear, or the shape of a head, perhaps a leg. Then the output is able to recognise the elephant. Each layer adds a step of clarity, a layer of construction. I guess the intuition here is that the initial layer blows up the input into its smallest components, which may be enough to go direct to an output layer. If the pattern you’re looking for is hidden under layers of complexity, then hidden layers are needed to use the pieces extracted from the input layer to build up something that can be recognised.
Training
I briefly touched upon the concept of training earlier: the process of choosing weights correctly such that the output of the net given a sample input is what is expected. I mentioned the gradient descent algorithm (walking down a hilly landscape to the basin - representing the minimisation of the error in results), but there are other optimisation algorithms:
- Newton’s method
- Conjugate Gradient
- Quasi-Newton
- Levenberg-Marquardt
- and more…
I’m going to use gradient descent as it is simple, and this is a simple neural network. Information on the others mentioned above in this article. Regardless of the optimisation method you use, the process is the same:
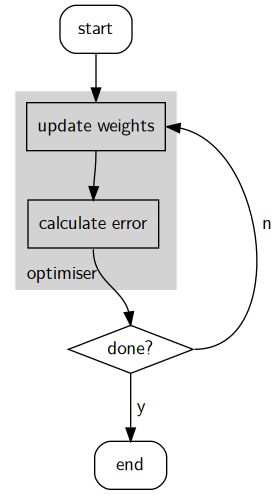
Update weight values using the optimiser, then check to see if we’re at an acceptably low error. If so, end. Otherwise, optimise again.
Error is calculated using a training dataset. This is a set of data which contains inputs, and the corresponding outputs. This could be a bunch of handwritten numbers as input, and the integer representation of the numbers as output. The error is a measure of how “far” the neural network’s output is from the expected output. This is measured over the whole of the training dataset: with each input and output pair adding to the total error.
One pass through the entire learning dataset is called an epoch.
As you can imagine, datasets are (normally) large. Very large. This can make computation of an epoch difficult, in which case it can be useful to split up the epoch into batches. The batches are iterated over until the epoch is calculated. This article goes in to more detail about the difference between epochs, batches, iterations…
Once the entire dataset is processed and the weights are updated, we may have a rough solution. How rough? We analyse this using the error.
We want the error to be zero, in an ideal world. However, this is not practical so we just want the error to be low. In fact, if the error was zero, then it is likely that we have overfit our network to our training dataset. This means that instead of learning how to do the generic action of converting input to output, it has learned to do the more specific task of converting training input into training output and it may not work on other, real world, data. (This is like a student studying the answers for an exam, not the method.)
With the threat of over-training, we need to train just enough to meet our target accuracy and no more. This has the added benefit of being computationally efficient: no wasting time getting to 0.0001% error, when 1% will do.
On the other hand, if we don’t train the network enough, we get underfitting: a poor performing neural network which mis-classifies too often.
Choosing the number of epochs, the right amount of training, is a difficult question. The answer I’ve found so far is to use trial and error. The choice of this forms part of a process called “hyper parameter optimisation” where you choose the best values for “hyperparameters” which affect how training proceeds.
Testing
I’m building up from nothing, so I’ll need some way of testing the network and the training process to check they’re working as expected. Luckily, this process is pretty much the same as the training process, involving the same data too. I’ll need a dataset of test inputs with their corresponding outputs. This means I can check the ‘net is working by training it against some members of the set, then verifying it with the rest of the set.
What sets this apart from just more training, is that the training algorithm itself will be analysed: does the error fall as training proceeds? If not, why not? What’s broken?
For this stage, I’ll need a variety of test data and sample networks. Starting from the absurdly simple linear regression case, moving up in complexity to something which closer resembles my end goal.
Simple Linear Regression
A linear function \(f(x)\) gives an output \(y\):
\[ y = f(x) = mx + c \]
This is the simplest case I could think of. The input layer has only a single neuron, as does the output. Therefore there is a single weight to find (the gradient) and a single bias (the intercept).
This case will test the training algorithm's ability to find and settle upon weights and biases.
Next in series (1)
Given a vector, a function $f(\vec{x})$ gives the next item in the series:
\[ x_{n+1} = f([x_{n} + x_{n-1} + x_{n-2} + ... + x_{2} + x_{1}]) \]
This is a little more abstract, a little more complex. The series in question is series of natural numbers (whole numbers from 1 to N):
\[ y_{i+1} = y_{i} + 1 \] \[ y_{1} = 1 \]
or
\[ y_{i} = i \]
Implementing a Neural Network
Alright, so how do we go about building a neural network? Well the quick answer is to use a library like Tensorflow, PyTorch, or anything else that floats your boat. The whole idea here however is that I’d like to start a bit lower to get a good grasp of how these higher level libraries are implemented, so I’ll build up in C++.
A quick recap: a neural network is composed of a bunch of neurons, organised into layers. The network performs a task, for which it is trained. The training process decides the value of the weight values for passing information forward from neuron to neuron.
A layer is composed of a number of neurons, each connected to every other neuron in the layer preceding it. The number of neurons in a successive layer is used to reduce complexity down to the final output. If a net is being designed to find an answer to a yes/no question, the final layer (before the output layer) might only have a few neurons, the output layer having only one (which fires for “yes” and is quiet for “no”).
Neuron
Let’s start with the basic building block: the neuron. This object will contain a reference to its input connections, and their associated weights.
// src/neuron.hpp
#pragma once
#include <vector>
namespace sinn {
class Neuron {
public:
Neuron() =default;
virtual ~Neuron() =default;
virtual double get_value() =0;
};
} // namespace sinnThe Neuron base class is never intended to be used directly, only through its sub-classes. The only common method through all Neuron sub-classes is get_value(), which calculates the value of a Neuron based on its weights, bias, and inputs. I’ve included this here as a pure virtual function, ready to be overridden by the sub classes.
This base class will provide a standard interface to the derived classes. (How great is polymorphism in C++?) With our base interface in place, let’s derive a neuron for the hidden and output layers:
// src/hidden_neuron.hpp
#pragma once
#include "neuron.hpp"
#include "activation_functions/activation_function.hpp"
namespace sinn {
class NeuralNetwork;
class HiddenNeuron : public Neuron {
private:
std::vector<Neuron *> in;
std::vector<double> weights;
std::vector<double> substitute_weights;
double bias;
double substitute_bias;
ActivationFunction *activation_function;
public:
HiddenNeuron(ActivationFunction *actfunc);
~HiddenNeuron() =default;
double get_value() override;
void add_weighted_input(Neuron *neuron, double weight);
void set_activation_function(ActivationFunction *activation_function);
double get_bias();
double get_substitute_bias();
double get_weight(int);
double get_substitute_weight(int);
void set_bias(double);
void set_substitute_bias(double);
void set_weight(int, double);
void set_substitute_weight(int, double);
void swap_weights_and_bias();
friend NeuralNetwork;
};
} // namespace sinnThe Hidden Neuron is a neuron in a hidden (or output) layer. These neurons take input from a previous layer of neurons, which are weighted and summed with bias to form an output. So in this header I’ve declared the override get_value() method, as well as methods for linking the neuron to an input Neuron, setting weights and biases, and setting the activation function.
The get_value() function is pretty simple, just adding the weighted values of the inputs:
// src/hidden_neuron.cpp
#include "hidden_neuron.hpp"
namespace sinn {
double HiddenNeuron::get_value()
{
double total = 0.0;
for (size_t i = 0; i < this->in.size(); i++) {
Neuron *neuron = this->in[i];
double weight = this->weights[i];
total += neuron->get_value()*weight;
}
return this->activation_function->calculate_value(total);
};
}; // namespace sinnThis is the main functionality of the hidden- and output-layer neurons: process information from an upstream layer of neurons. What about the input? For this implementation, input “neurons” are just placeholders, taking a value and returning it as their own.
// src/input_neuron.hpp
#pragma once
#include "neuron.hpp"
namespace sinn {
class InputNeuron : public Neuron {
private:
double value;
public:
InputNeuron(double value);
~InputNeuron() =default;
double get_value() override;
void set_value(double value);
};
} // namespace sinnThe constructor this time takes a value as input, which the neuron can then return when asked for its value:
namespace sinn {
InputNeuron::get_value()
{
return this->value;
}
} // namespace sinnLayer
Next up, organising neurons into Layers. Layers, for this API, are nice ways of constructing a number of neurons with specified weights.
As with the Neuron, I’ll start with an abstract base which will be overridden by more specific sub-classes:
// src/layer.hpp
#pragma once
#include <vector>
#include "neuron.hpp"
namespace sinn {
class NeuralNetwork;
class Layer {
protected:
std::vector<Neuron *> neurons;
public:
Layer() =default;
virtual ~Layer();
void add_neuron(Neuron *neuron);
void clear_neurons();
friend NeuralNetwork;
};
} // namespace sinnA Layer consists of a vector of Neurons, and that’s it. It’s friends with the NeuralNetwork class, good for them. (It’s handy to be able to access Neurons directly from the NN.)
Nothing really special here. As with the Neurons there are Input and Hidden derived classes, however there is also an Output derivation. The HiddenLayer subclass is just to keep the nomenclature the same, really, bar a small generate_neurons(int n) method which allows for the easy creation of neurons:
// src/hidden_layer.hpp
#pragma once
#include "hidden_neuron.hpp"
#include "layer.hpp"
namespace sinn {
class HiddenLayer : public Layer {
public:
HiddenLayer(int n);
~HiddenLayer() =default;
void generate_neurons(int n);
};
} // namespace sinnThe InputLayer is a little more different, constructed with not a number of neurons, but a vector of the values for the InputNeurons that make up the layer:
#include "input_layer.hpp"
namespace sinn {
InputLayer::InputLayer(std::vector<double> input_values)
{
this->generate_neurons(input_values);
}
InputLayer::InputLayer(int n)
{
this->generate_neurons(n);
}
void InputLayer::generate_neurons(std::vector<double> input_values)
{
for (auto value : input_values) {
InputNeuron *n = new InputNeuron(value);
this->add_neuron(n);
}
}
void InputLayer::generate_neurons(int n)
{
for (int i = 0; i < n; i++) {
InputNeuron *n = new InputNeuron(0.0);
this->add_neuron(n);
}
}
} // namespace sinnAnd the OutputLayer:
#include "output_layer.hpp"
namespace sinn {
std::vector<double> OutputLayer::get_output()
{
std::vector<double> rv;
for (auto n : this->neurons)
rv.push_back(n->get_value());
return rv;
}
} //namespace sinnNetwork
With the organisational stuff out of the way, on to the meat of the thing! The NeuralNetwork is a network of Neurons, abstracted through Layers. I suppose the Network class is another “organisational thing”, but this one does stuff too! It takes data (vector of float) and processes through the network and returns the result. Also, it can learn!
#pragma once
#include <string>
#include "layer.hpp"
namespace sinn {
class NeuralNetwork {
private:
std::vector<Layer *> layers;
double last_error;
public:
NeuralNetwork();
// nn_print.cpp
void print();
// train.cpp
void train(std::vector<std::vector<double>> training_inputs, std::vector<std::vector<double>> training_outputs, double learning_rate, double dWeight=1e-5);
double get_error(std::vector<std::vector<double>> training_inputs, std::vector<std::vector<double>> training_outputs);
// nn_dot.cpp
void as_dot(std::string filename) const;
// neural_network.cpp
void link_layers_weighted(int, int, double);
void link_layers_normal(int, int, double, double);
void link_layers_uniform(int, int, double, double);
void add_layer_weighted(Layer *layer, double weight);
void add_layer_normal(Layer *layer, double, double);
void add_layer_uniform(Layer *layer, double, double);
void set_input(std::vector<double> input);
double get_last_error() const;
std::vector<double> get_output() const;
std::vector<double> get_output(std::vector<double> input);
std::vector<double> operator()(std::vector<double> input)
{
return this->get_output(input);
}
};
} // namespace sinnNotable methods here are train() and get_error().
Layers are added one by one, starting from the furthest upstream (an InputLayer). As they are added, their Neurons are linked together, forming the Network:
// src/neural_network.cpp
#include <iostream>
#include <sstream>
#include <fstream>
#include "util.hpp"
#include "exception.hpp"
#include "hidden_neuron.hpp"
#include "neural_network.hpp"
#include "input_neuron.hpp"
#include "output_layer.hpp"
namespace sinn {
void NeuralNetwork::add_layer_weighted(Layer *layer, double weight)
{
this->layers.push_back(layer);
size_t nlayers = this->layers.size();
if (nlayers > 1) {
for (auto previous : this->layers[nlayers-2]->neurons) {
for (auto latest : this->layers[nlayers-1]->neurons) {
((HiddenNeuron *)latest)->add_weighted_input(previous, weight);
}
}
}
}
}; // namespace sinnThere are other forms of the add_layer..() function which generate a random starting weight (uniform or guassian), but the plain one here takes in a starting weight as given.
The final layer should be an OutputLayer, completing the network streaming data from Input to Output.
Gradient Descent
Gradient descent is the training process of measuring the error’s rate of change with respect to the weights/biases, and altering the weights/biases accordingly. This starts with calculating the Error for the current set of weights and biases. A training dataset (i.e., one with solutions) is passed through the Network, and the error is calculated as the sum of the square of the difference between the calculated output and the desired output.
// src/train.cpp
#include <iostream>
#include "neural_network.hpp"
#include "hidden_neuron.hpp"
#include "output_layer.hpp"
#include "util.hpp"
namespace sinn {
double NeuralNetwork::get_error(std::vector<std::vector<double>> training_inputs,
std::vector<std::vector<double>> training_outputs)
{
if (training_inputs.size() != training_outputs.size()) {
std::cerr << "net::get_error: training dataset inputs must match size of outputs." << std::endl;
}
double total_error = 0.0;
for (size_t set_index = 0; set_index < training_inputs.size(); set_index++) {
auto input = training_inputs[set_index];
auto output = training_outputs[set_index];
std::vector<double> value = this->get_output(input);
total_error += sinn::util::sumsqdiff(value, output);
}
this->last_error = total_error;
return total_error;
}
} // namespace sinnThe error can be calculated before and after a small change (perturbation) is made to a weight/bias: the rate of change of the error with respect to that weight or bias can be approximated from:
[ \frac{dError}{dWeight} \approx \frac{\Delta{}Error}{\Delta{}Weight} = \frac{Error_{after} - Error_{before}}{Perturbation_{Weight}} ]
Using the gradient, a required change in that weight or bias can be calculated:
[ dWeight = -\frac{dError}{dWeight}\eta ]
Where $\eta$ is the learning rate (another hyperparameter). This is the descent part, the rate of change is like a steepness, and the learning rate is a step size. We want to walk down the hill, so there’s a negative sign in front. This desired change is stored until all the gradients have been calculated, then it is enacted. This process should reduce the error to an acceptably low value.
// src/train.cpp
#include <iostream>
#include "neural_network.hpp"
#include "hidden_neuron.hpp"
#include "output_layer.hpp"
#include "util.hpp"
namespace sinn {
void NeuralNetwork::train(std::vector<std::vector<double>> training_inputs,
std::vector<std::vector<double>> training_outputs,
double learning_rate,
double dWeight)
{
double initial_error = this->get_error(training_inputs, training_outputs);
for (size_t layer_index = 1; layer_index < this->layers.size(); layer_index++) {
auto layer = this->layers[layer_index];
for (auto _neuron : layer->neurons) {
HiddenNeuron *neuron = ((HiddenNeuron *)_neuron);
for (size_t weight_index = 0; weight_index < neuron->weights.size(); weight_index++) {
double weight_before = neuron->weights[weight_index];
neuron->weights[weight_index] += dWeight;
double dError = this->get_error(training_inputs, training_outputs) - initial_error;
neuron->weights[weight_index] = weight_before; // done in this way to prevent possible
// floating point errors introduced by
// adding and subtracting
double gradient = (dError == 0) ? 0 : dWeight/dError;
neuron->set_substitute_weight(weight_index, weight_before - (learning_rate * gradient));
}
{
double bias_before = neuron->get_bias();
neuron->set_bias(bias_before + dWeight);
double dError = this->get_error(training_inputs, training_outputs) - initial_error;
neuron->set_bias(bias_before);
double gradient = (dError == 0.0) ? 0.0 : dWeight/dError;
neuron->set_substitute_bias(bias_before - (learning_rate * gradient));
}
}
}
for (size_t layer_index = 1; layer_index < this->layers.size(); layer_index++) {
auto layer = this->layers[layer_index];
for (auto _neuron : layer->neurons)
((HiddenNeuron *)_neuron)->swap_weights_and_bias();
}
this->get_error(training_inputs, training_outputs);
}
}; // namespace sinnDemonstration
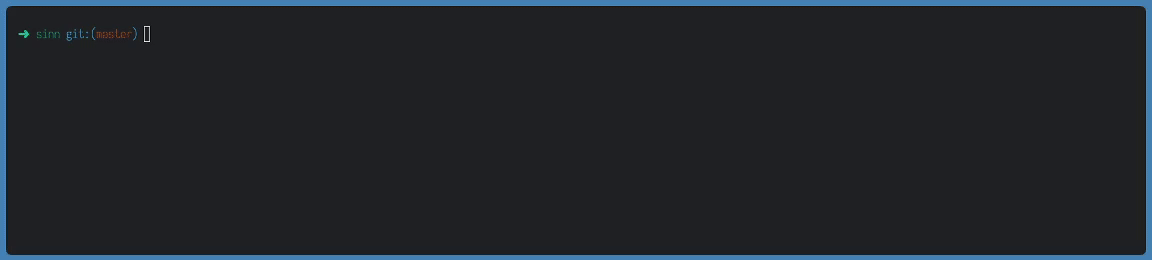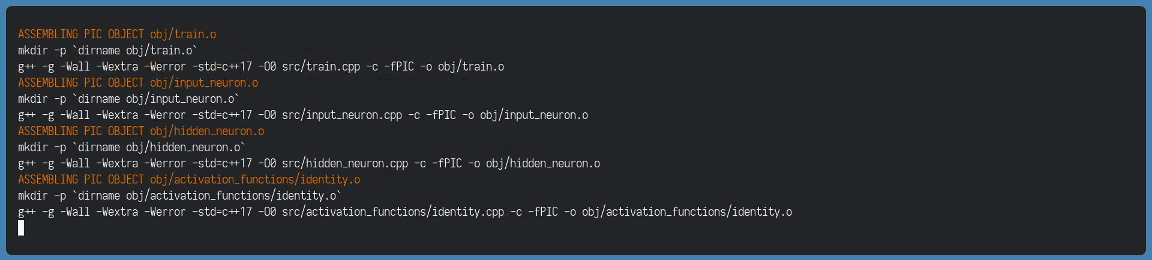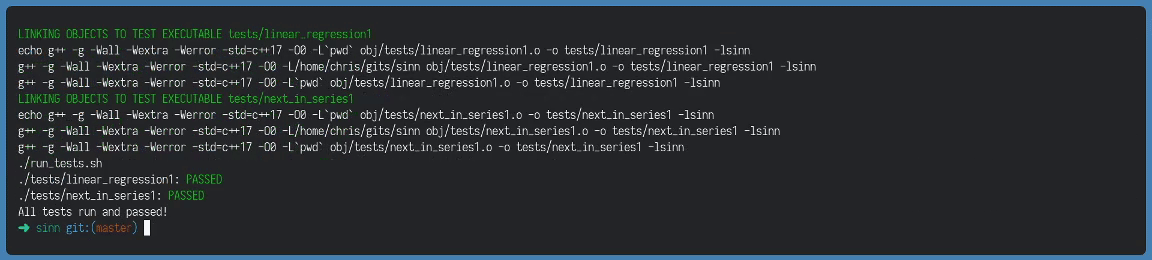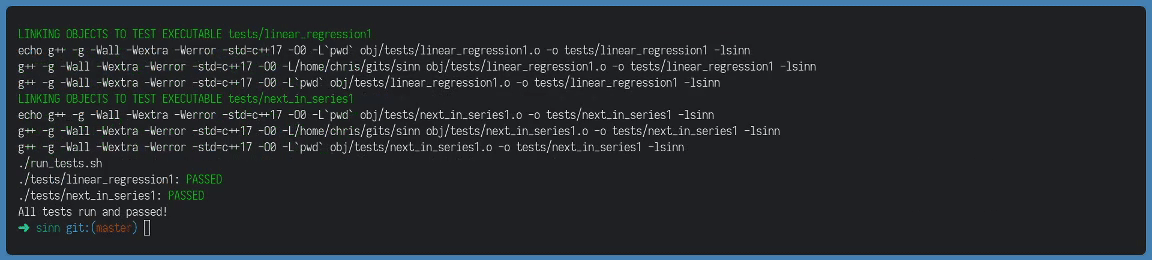
In the repository I have some tests prepared for the very simple test-cases outlined above. To run them, clone the repo and just make. It depends only on gcc. The test cases are the two discussed above. Here’s an underwhelming gif of the network being built and the tests being run:
Closing remarks
In this post I’ve shown how simple a neural network can be, in my simple literal implementation. There are many improvements that could be made (back propagating learning, fewer abstractions, better testing), but sadly I lack the time.
Resources
Some useful resources on Neural Networks:
- gentle introduction to neural networks series (GINNS) - part 1 - https://towardsdatascience.com/a-gentle-introduction-to-neural-networks-series-part-1-2b90b87795bc
- GINNS2 - neural network from scratch - https://towardsdatascience.com/build-neural-network-from-scratch-part-2-673ec7cdd89f
- (GINNS) ends here - author didn't finish it, last post in 2017.
- network + weights + activation function?
- quick ml terminology - https://hackernoon.com/everything-you-need-to-know-about-neural-networks-8988c3ee4491
- beginner's guide to activation functions - https://towardsdatascience.com/secret-sauce-behind-the-beauty-of-deep-learning-beginners-guide-to-activation-functions-a8e23a57d046
- "building a silicon brain" - https://www.the-scientist.com/features/building-a-silicon-brain-65738
- "Machine, Learning, 1951" (cool photograph of neuron) (what's with the odd comma placement?) - https://www.the-scientist.com/foundations/machine--learning--1951-65792
- examples of keras networks - https://github.com/keras-team/keras/tree/master/examples
- "Neural Network Design" by Hagan, DeMuth, Beale and De Jesus.
- "Epoch vs Iterations vs Batch size" - https://towardsdatascience.com/epoch-vs-iterations-vs-batch-size-4dfb9c7ce9c9
- tiny-dnn: header-only dependency-free deep learning neural network library - https://github.com/tiny-dnn/tiny-dnn
